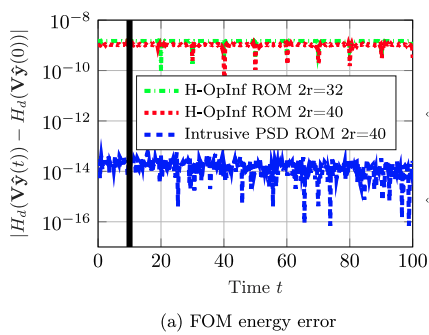
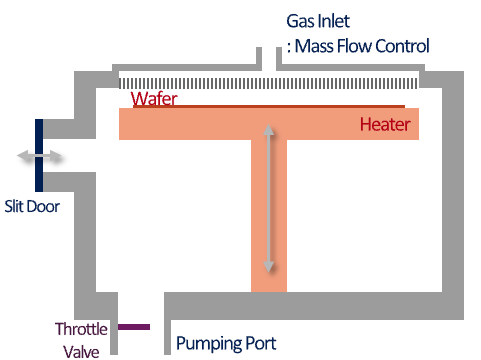
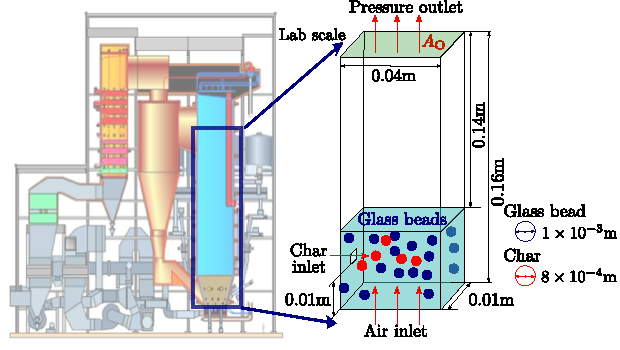
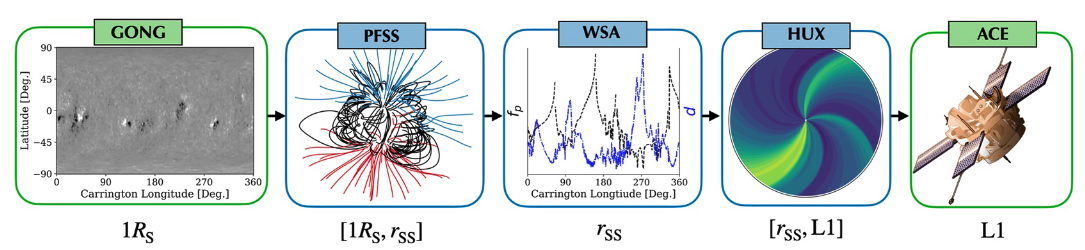
Research Summary

Our group is working on computational methods and numerical analysis for control, uncertainty quantification and optimization of complex and large-scale dynamical systems. Specifically, our research centers around reduced-order modeling and it's applications in many-query settings. Within reduced-order modeling we work on linear and nonlinear techniques and projection-based and fully data-driven, specifically on structure preservation (Lagrangian, Hamiltonian, gradient structure, port-Hamiltonian), system theoretic model reduction (e.g., balanced truncation, eigensystem realization) and also proper orthogonal decomposition. Within uncertainty quantification, we work on coherent risk estimation and certified risk-based design optimization (with conditional value-at-risk and buffered probabilities), reliability-based design optimization, multifideltiy UQ methods, and Bayesian inference. Working mainly in methods development, our research is interdisciplinary, both with respect to computational-science domains (computer science, engineering, mathematics) and applications (reactive and non-reactive fluids, cell biology, soft robotics, space weather, continuum mechanics, plasma physics, etc).



Research Topics

Nonlinear Model Reduction

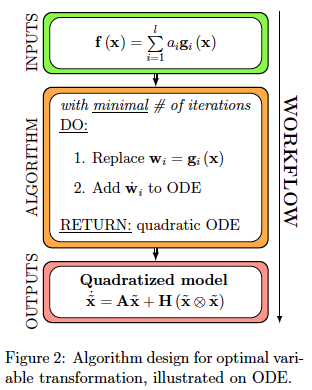
Using systems theory, mathematical approximation theory, and data science, we reduce the complexity of high-dimensional distributed systems via projection in the time domain, interpolation in the frequency domain, or by learning reduced-order models purely from a variety of data. Specifically, my group's research centers around:

  • System-theoretic Model Reduction for Control: This branch of model reduction uses classical principles such as controllability/observability, pole/residue approximations, Lyapunov stability, positive-realness and others to derive reduced-order models, mostly for controlled (open or closed-loop) systems. Our work mostly focused on nonlinear balanced truncation model reduction ([J17, J19, J35, J41, J45, C12, PP01]) Moreover, we developed extensions of eigensystem realization coupled with tangential interpolation ([J01]) as well as fast CUR matrix decompositions ([J07]) to learn ROMs from impulse response data. The resulting ROMs can be used to design controllers and observers, as they have favorable system-theoretic properties.
  • Structure-preserving Model Reduction: Operator Inference (see our 2024 survey [J32]) uses simulated, observed, or experimental data to infer low-dimensional models evolving on subspaces or manifolds. The structure of the ROM operators leverages physical insights, such as the polynomial degree of mechanisms, conservation principles, invariences, symmetries, etc. Our work suggests embedding Lagrangian structure of second-order systems [J33, J34, C11, C13], Hamiltonian principles [J21, J29, J36], Lyapunov stability ([J18, J25]), shift-invariance ([J23]), to enforce hard state constraints ([J50]), and to have conservative models for plasma simulations ([J47]), and others. Moreover, we have developed Bayesian system identification techniques for stochastic Hamiltonian ROMs ([J40,C10]). Creating this structure in ROMs is key for long-term predictive models and can be used for energy-based control.
  • ROM Closure Modeling: As frequently observed, due to the truncated dynamics and energy transfer, ROMs can become unstable for complex fluid problems. In these situations, additional closure models are needed to stabilize the system while keeping the model dimension low. In a series of works, we developed closure models for ROMs that removed the need for heuristics and combines data and a parametrized model term to determine the closure; this was then demonstrated to successfully stabilize a 3D fluid flow ([J06, C03, C05]). Recently, we also derived closure models for collisionless plasma models through approximating higher-order moments with a ROM ([J47]).

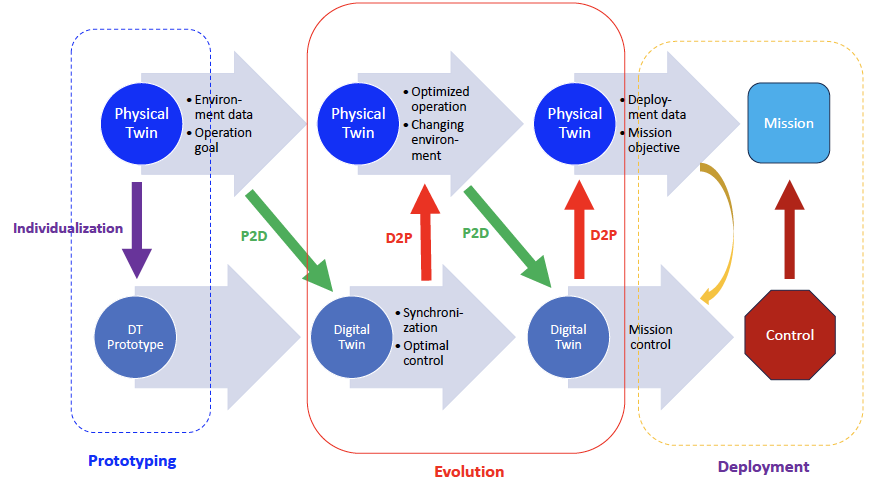
    • Control of High-dimensional and Distributed Systems

    While deriving a nonlinear ROM with system-theoretic properties and then deriving a controller can be very successful (``reduce-then-design"), we also worked on a variety of control approaches that directly work on the high-dimensional system (``design-then-reduce), as well as a variety of other control approaches:

  • Polynomial-polynomial Regulator (PPR): We recently developed new computational techniques for the PPR problem ([C15, J41]) based on series expansions and tensor solutions of the Hamilton-Jacobi-Bellman equations, where we solve for nonlinear feedback control in over 1,000 dimensions, leading to linear systems that need to be solved for the feedback law with matrices of over 100,000,000,000 dimensions. We solve those with Kronecker-form expansions of QR factorizations along with block-backsubstitution methods and low-level BLAS operations.
  • Quadratic Recasting: Evolutionary processes in engineering and science are often modeled with nonlinear non-autonomous ordinary differential equations that describe the time evolution of the states of the system, i.e., the physically necessary and relevant variables (c.f., the short survey [J22]). However, these models are not unique: the same evolutionary process can be modeled with different variables. This can have tremendous impact on computational modeling and analysis. The idea of recasting in via variable transformation (referred to as lifting when extra variables are added) to promote model structure is found across different communities, with literature spanning half a century. Our group is interested in exploring variable transformations for ROM learning ([J12, J14, C06, C09]), discovery and exploitation of structure ([J19, J51]) and especially designing algorithms and provable guarantees for finding such transformations ([J31]).
  • Linear-Quadratic Regulator (LQR) and Nonlinear Iterative LQR: We worked on scalable solutions to LQR and iterative LQR approaches through projection-based solvers for Riccati equations ([J02]) in 100,000s of dimensions, learning-based LQR control for parameter-dependent distributed systems ([J05]), LQR control of coupled PDEs ([C02, C04]), and iterative LRQ for nonlinear systems ([J17]).

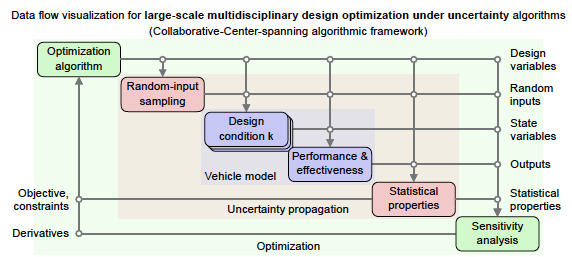
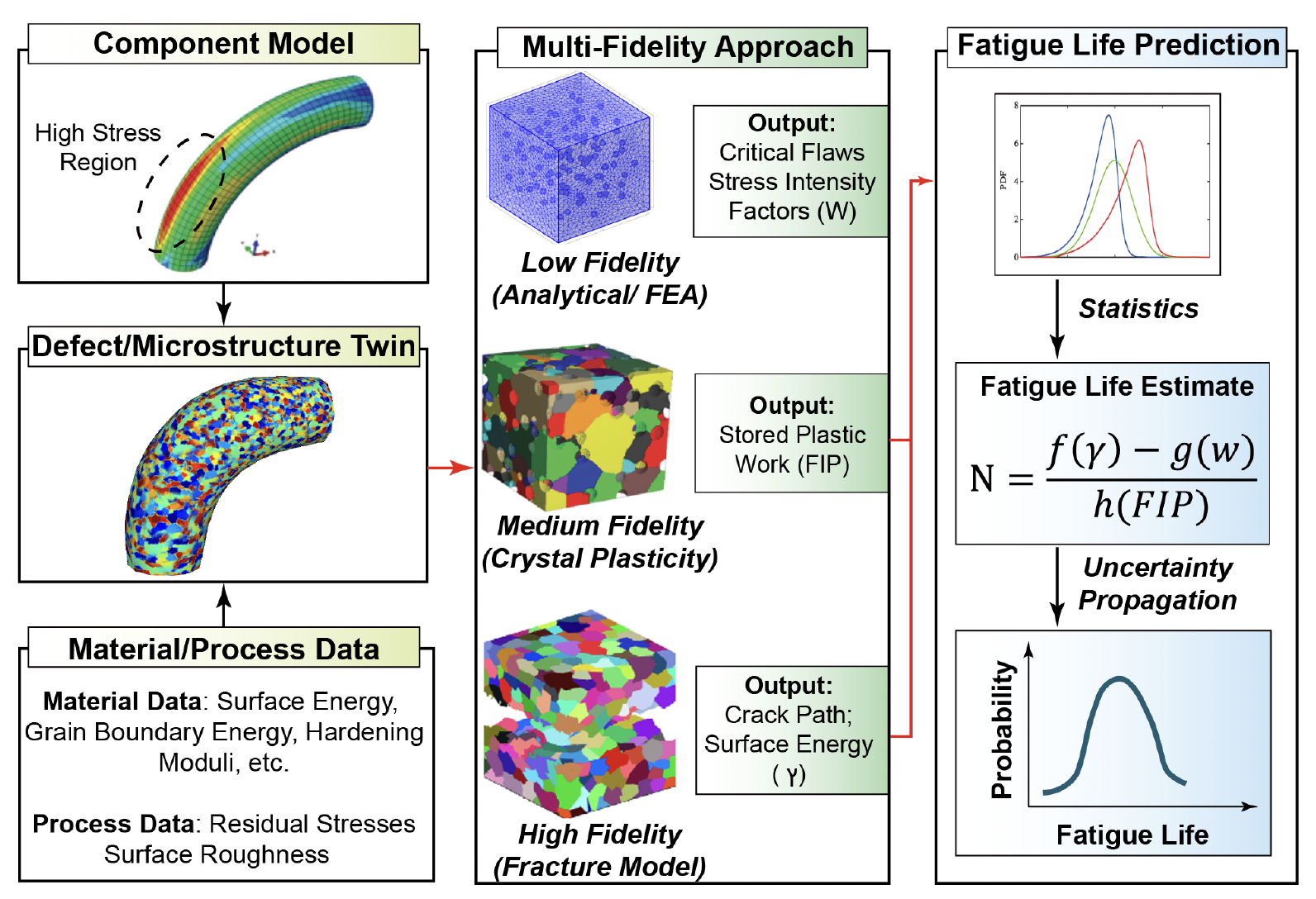
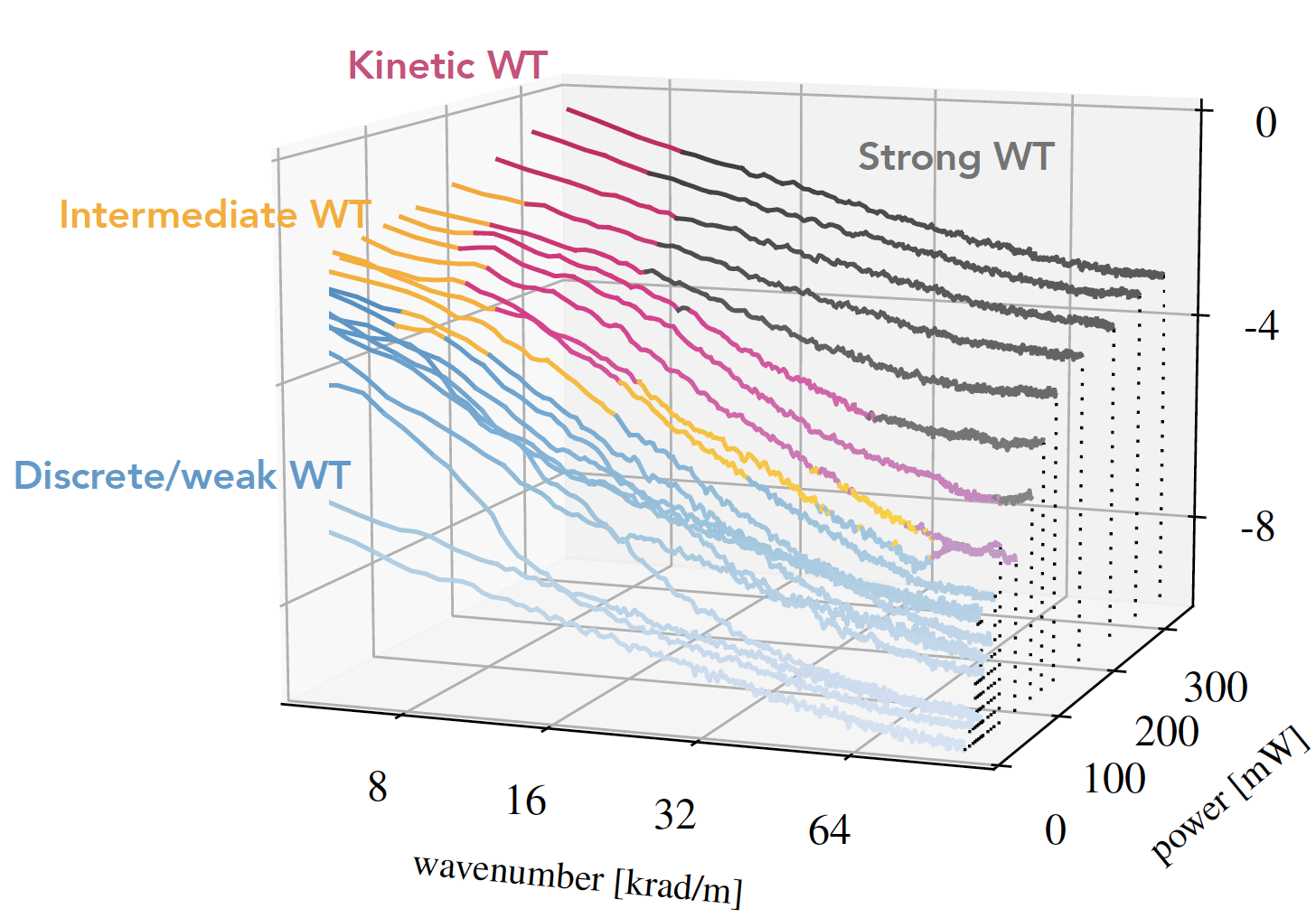
    • Multifidelity uncertainty quantification (UQ) and design under uncertainty

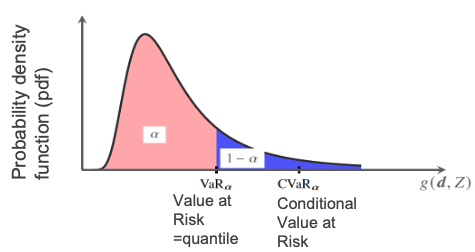
    In the presence of parametric and model form uncertainty, quantifying and managing uncertainties is key for decision makers and engineers. One aspect of this area focuses on computing statistical information such as mean and variance, or other information about the distribution of quantities of interest, such as coherent risk measures (CVaR, buffered probabilities, see [J20]). Traditionally, this would often require a large number of expensive model evaluations, rendering high-fidelity models infeasible to be used for this task. Multifidelity UQ leverages information from models of varying fidelity and computational cost to efficiently solve the UQ task at hand. Such methods are attractive as they move most of the computational work to lower fidelity models and decrease the number of expensive high-fidelity model evaluations. In this area, our research connects often with reduced-order modeling and more generally statistical surrogate modeling, as follows:

  • Coherent risk measures for certifable design optimization: Coherent risk measures follow a set of axioms to arrive at a principled way to estimate tail risk ("black swans", "unwanted outcomes") which can often derail projects and cause catastrophic failure. By their nature of being rare, tail measures are hard to evaluate. We have developed a suite of surrogate-model-assisted risk estimators based on reduced-order models ([J09, J15]) and polynomial dimensional decomposition (PDD) for dependent random inputs ([J26, J27]). Moreover, we worked on design with risk measures ([J20, C07, J48]).
  • Bayesian Uncertainty Quantification: The Bayesian perspective to inference starts with an intitial belief state and updates this belief as new information becomes available. These updates require many model evaluations, which are expensive for PDE models. Our group has worked on Bayesian and multimodel inference in the context of systems biology ([J24, J46, J49]), composite failure modeling ([J28]), space weather ([J30]) and Bayesian model learning of Hamiltonian systems ([J40, C10]).
  • Design Under Uncertainty: Besides risk measures, sometimes reliability thresholds and mean and variance reduction may sometimes be the preferable way to formulate a DUU problem. There, multifidelity approaches save orders of magnitudes of computational cost when evaluating probabilistic constraints within the design optimization loop, see ([J43]). Moreover, work on reusing information from past design iterations has also helped reduce the computational cost of RBDO ([J13]).

    • Current Projects

    image
    Collaborative Research: Nonlinear Balancing: Reduced Models and Control (NSF Grant 2130727; 01/01/2022-12/31/2024; in collaboration with Profs. Jeff Borggaard and Serkan Gugercin, Virginia Tech). In this project, we develop a new class of reduced-order models and controllers for complex high-dimensional polynomial nonlinear systems via the concept of nonlinear balanced truncation. Specifically, we developed a scalable tensor-based approach to solve the HJB equations required for nonlinear balancing for a class of polynomial control-affine systems, to obtain polynomial expansions of the energy functions required for balanced truncation, as well as high-performance algorithms and numerical analysis to analyze the conditioning of the tensorized problems. Additionally, reduced-order nonlinear controllers are designed using a simultaneous reduction and control framework, which is far superior to the existing reduce-then-control framework. Phd Student Nick Corbin is working on this project.

    image
    CAREER: Goal-oriented Variable Transformations for Efficient Reduced-order and Data-driven Modeling (NSF Grant 2144023; 05/01/2022-04/30/2026). In this project, we develop the foundations of a new theoretical and computational paradigm that leverages variable transformations to uncover low-dimensional structures in nonlinear dynamical systems and achieve efficient and accurate model reduction that may be certified with respect to stability and structure-preservation. We approach this in model- and data-driven settings by designing symbolic computing algorithms that systematically identify transformations and subsequent order-reduction projections that result in optimal quadratic or polynomial models that also preserve symplectic structure for Hamiltonian systems. In the data-driven case, transformations are sought that lead to long-term predictive reduced-order models that are physically interpretable and have favorable numerical properties. Through this effort, new low-dimensional models of the physics of medium-scale applications of chemical reaction dynamics and additive manufacturing will be discovered. The methodological contributions will be assessed on large-scale models of reactive flows and ocean dynamics. PhD student Albani Oliveiri and undergraduate student Anique Dittrich are working on this project.

    image
    MURI: Mathematics of Digital Twins. (Air Force Office of Scientific Research.; 09/2024-10/2029). For a high-level overview, see the UC San Diego Today article . In this project, we will develop task-oriented (parametric and system-theoretic) reduced-order models for digital twin development, with a focus on metal-additive manufacturing.

    image
    ACCORD: AFRL–UCSD Collaborative Center for Optimal Risk-quantified and robust Design of aerospace vehicles. (Air Force Research Lab.; 12/08/2023-09/07/2029). The ACCORD center will revolutionize the design of next-generation aerospace vehicles through new computational design methods centering around large-scale multidisciplinary design optimization (MDO); for a high-level overview, see the UCSD News article New Center Supports Next-Gen Air Force Vehicle Design. The center is led at UCSD by Professor John Hwang, and co-PIs are Professors Oliver Schmidt and J.S. Chen (SE). Professor Markus Rumpfkeil at U. of Dayton is also collaborating on this project. Our research group will contribute with reduced-order modeling for coupled systems as well as by providing new tools for surrogate-assisted risk-based design optimization at scale.
    image
    Predictive Real-Time Intelligence for Metallic Endurance (PRIME). (DARPA; 02/03/2025-02/02/2027). The PRIME project aims to develop a physics-based digital twin interface for uncertainty-quantified lifetime prediction of parts produced using laser powder bed fusion (LPBF) additive manufacturing. The multidisciplinary team (University of Michigan, Texas A&M University, Auburn University, UCSD, along with key industry partners including Addiguru, AlphaStar, and ASTM International) will collaborate on innovative developments, including multi-sensor data fusion for real-time defect detection, accelerated physics modeling using Kalman state estimation and machine learning, digital twins capturing microstructures at scales not currently possible, and comprehensive fatigue life assessment combining microstructure-based life models with multi-fidelity uncertainty quantification. Currently, LPBF lacks accurate lifetime predictions due to uncertainties in defects, microstructure, and fatigue behavior. Existing approaches rely on empirical models or simplified simulations, limiting their accuracy. If successful, PRIME’s impact lies in revolutionizing additive manufacturing by delivering a user-friendly digital twin package for lifetime prediction of LPBF parts with transferability across different platforms, ultimately allowing low-cost distributed production of critical parts. More information here.
    image
    STORMLAP: Strong Turbulence and Rogue-Wave Modeling using Machine-Learning Assisted Predictions (DARPA; 03/17/2025-03/16/2026). In this project, we plan to (1) develop an innovative tabletop simulator (experiment) for training ML systems on a highly turbulent phenomena and (2) to provide a framework for more broadly training ML on turbulence phenomena arising from weakly to strongly nonlinear phenomena of all kinds. With this approach, we overcome current limitations in modeling turbulent fluid dynamics through expensive direct numerical simulation by providing a tabletop experimental model of tunable turbulence. The experimental model will produce datasets with unprecedented spatiotemporal resolution using high-speed digital holographic microscopy (HSDHM), which are ideal for training ML on a difficult but defined problem: capillary wave dynamics. While many forms of turbulent phenomena exist, our example of tunable capillary wave turbulence is ideal for quick adoption in ML training as an outwardly simple, tabletop experiment with extraordinary complexity in its response to vibration excitation.
    image
    Center for Advancing the Radiation Resilience of Electronics (DOE NNSA PSAAP IV, 09/15/2025-09/14/2030). CARRE is a multidisciplinary research center dedicated to advancing predictive simulation of radiation damage in electronic systems. By integrating multiscale, multiparticle physics with cutting-edge AI and exascale computing, we aim to reduce reliance on physical testing and accelerate innovation in electronics resilience. The demands for future engineered systems to withstand normal and extreme off-normal radiation environments, both in space and in terrestrial applications, requires a predictive capability supported by advanced algorithms and software engineering that can take advantage of exascale computing resources. This problem is inherently multiscale and multiphysics—involving material response to radiation from the atomistic to macroscopic level. Our simulations will be validated by experiments designed, performed, and analyzed by our team. Our research will directly impact exascale computing programs involving stochastic solvers, particle transport, and the understanding of radiation response of electronics in environments of interest to the NNSA. From CubeSats to autonomous vehicles, CARRE’s work supports critical applications in national security, space exploration, and high-performance computing.
    image
    Simulation & Design of Heterogeneous Architectures for Performance and Energy Absorption (DOE NNSA PSAAP IV,09/15/2025-09/14/2030). The SHAPE Center (Simulation & Design of Heterogeneous Architectures for Performance and Energy Absorption) is a multi-disciplinary research hub dedicated to the development of the scientific understanding and computational methods needed to enable the design of materials that currently lie outside the reach of conventional approaches. Our vision is to establish the methodologies by which new classes of material systems tailored for impact events can be discovered and designed. The Center pursues an integrated program in which: (i) Design optimization is coupled with predictive physical models to identify architectures with targeted properties. (ii) Uncertainty quantification and robust optimization ensure reliability of designs under variability and incomplete knowledge, (iii) High-fidelity simulation methods with scientific machine learning capture the nonlinear, multiphysics phenomena central to impact events, (iv) Exascale computing platforms provide the computational power needed to explore and expand design spaces.More info also on UCSD Today.

    Past Projects

    image
    Nonlinear Data-driven and Structure-Preserving Hamiltonian Model Reduction (ONR Grant N00014-22-1-2624; 08/01/2022-07/31/2025). Computational modeling, simulation and control of physical systems characterized by Hamiltonian mechanics abound in naval applications, such as ocean flow modeling, plasma physics, and continuum mechanics models that follow a principle of least action. From a mathematical perspective, Hamiltonian systems have additional physical and geometric structures in the form of symmetries, symplecticity, first integrals, and energy preservation. Those properties need to be preserved in time and space discretization, and particularly in data-driven reduced-order modeling, which this project is concerned with. Specifically, we are developing nonlinear structure-preserving data-driven reduced-order modeling strategy for Hamiltonian systems. At UCSD, Postdoc Harsh Sharma is working on this project, with contributions from undergraduate student Juan-Diego Draxl. Our collaborator Zhu Wang (U. South Carolina) is a subaward on this project. Journal publications [29, 32, 33, 34, 36, 40] and conference publications [10, 11, 13] reflect this project.

    image
    Reduced-Order Modeling for Real-time Simulation of Flow Phenomena in Semiconductor Manufacturing. (Samsung Electronics Co.).; 03/15/2024-03/30/2025). This proposed collaborative project provides both training to the Visting Industry Fellow Dr. Seunghyon Kang as well as new research in surrogate modeling for flow phenomena occurring during semiconductor manufacturing. We will mainly focus on data-driven reduced-order modeling via operator inference. Postdoc Harsh Sharma and graduate student Hyeonghun Kim are partly contributing to this project.

    image
    Prediction, damage analysis and risk assessment for a gas power plant via fast and accurate reduced models. (Korea Institute for Advancement of Technology (KIAT) through the International Cooperative R&D program (No. P0019804, Digital twin based intelligent unmanned facility inspection solutions).; 12/01/2021-11/30/2024). This project involved BS & MS student Elle Lavichant, Postdocs Dongjin Lee and Harsh Sharma, as well as graduate student Hyeonghun Kim.

    image
    SWQU: Composable Next Generation Software Framework for Space Weather Data Assimilation and Uncertainty Quantification (NSF Award 2028125; 09/01/2020-08/31/2024). In this collaborative project with experts in geospace sciences (R. Linares, MIT; A. Ridley, UMich; Phil Erickson, MIT Haystack), uncertainty quantification (Y. Marzouk, MIT), fluid mechanics (J. Peraire, MIT), and software development (A. Edelman, MIT) we developed a variety of computational models and techniques for space weather prediction; see the UCSD news article Making space weather forecasts faster and better. Another article about space weather modeling that mentions our work appeared in Science News Solar storms can wreak havoc. We need better space weather forecasts. Journal publications [30,31, 39] were produced as part of this project. Phd student Opal Issan spent her first three years on this project, working on reduced-order modeling and uncertainty quantification for solar wind propagation.

    image
    Multifidelity Risk Assessment of High-Performance Systems. (DARPA, 08/20/2021-12/31/2022). In this project we developed surrogate-assisted methods for estimating coherent risk measures, such as conditional value-at-risk for complex engineering systems. We proposed bifidelity and multifidelity techniques that work in the context of depenent random variables. The surrogate models were developed as the dimensionally-decomposed generalized polynomial chaos expansions, with novel twists on how to train them effectively and use them in risk estimation. Journal publications [26, 27] resulted from this project. Postdoc Dongjin Lee worked on this project.

    image
    Newton Award for Transformative Ideas during the COVID-19 Pandemic (07/01/2020-12/31/2020). This 6-month project together with Prof. Melvin Leok (UCSD, Mathematics) developed ideas for a novel framework and mathematical formulation for systematic, robust, and efficient multi-fidelity modeling of large-scale hierarchical interconnected systems. We explored the combination of geometric structure-preserving numerical integration and model reduction in the context of hierarchical interconnected systems. Refer to the news article Mathematician, Engineer receive Newton Award for Transformative Ideas during COVID-19 Pandemic for more info.

    image
    SBIR Phase I: Human-Centered, Augmented Intelligence Software for Water and Wastewater (NSF Award 2004275 via Confluency LLC, Chicago; 07/01/2020-06/31/2020). This Small Business Innovation Research (SBIR) Phase I project developed methods for combining multi-fidelity simulation models and data-driven models to support decision-making for both long-term planning needs and real-time operational decision support for water and wastewater systems. Specifically, we investigated the reduced-order modeling for the St Venant equations for the one- and two-dimensional flow in waterways. The figure on the left shows a Lagrangian particle simulation for a storm wave travelling through a channel. MS student Liezl Maree worked on this project.